$\mathbb{X}$ yine $\mathcal{S}$ durum uzayına ve $P$ geçiş matrisine sahip bir Markov Zinrici olsun. Markov zinciri zamanla bir durumdan diğerine $P$'de verilen olasılıklarla geçiyor. Herhangi bir $j$ durumundan ilk kez geçtiği zamana 'ilk geçiş zamanı' olarak adlandıracağız ve bu zaman aşağıdaki gibi tanımlıyoruz:
$$T_j = min \{n \in\mathbb{N}: \hspace{0.5cm} X_n = j\} \tag{1}$$Markov Zinciri bu noktadan birden fazla kez (hatta sonsuz kere) geçiyor olabilir, biz bunların minimumunu alıp buna ilk geçiş zamanı $T_j$ diyoruz.
Soru: Eğer zincir $i$ durumundan başladığında, ileriki bir zamanda $i$'ye tekrar gelmek zorunda mı? Geliyorsa ne kadar sık geliyor?
Tanım: Bir $i$ durumu için
$$ \mathbb{P}(T_i < \infty) = \mathbb{P}(T_i < \infty | X_0 = i) = 1 \tag{3}$$ ise $i$ durumuna 'tekrar eden' (recurrent) durum denir.
Tanım: Eğer bir durum 'tekrar eden' bir durum değilse ona 'geçici' (transient) durum denir.
Teorem: Bir $i$ durumu ancak ve ancak aşağıdaki şart sağlanıyorsa 'tekrar eden' bir durumdur:
$$\sum_{n = 0}^{\infty} \mathbb{P}_{i, j}(n) = \infty \tag{4}$$Yukarıdaki ifadede $\mathbb{P}_{i, j}(n)$, terimi $i$ durumundan $j$ durumuna $n$ adımda geçme olasılığını gösteriyor. Eğer bir durum 'tekrar eden' bir durumsa, yani zincirin o duruma tekrar gelme ihtimali 1 ise, sonsuz adımda buraya sonsuz kere geleceğinden, tekrar tekrar geldiği adımlar için olasılıkları topladığımızda sonsuz elde edeceğiz. Bunu kanıtlamak için 'üreteç fonksiyonları' (generating functions) kullanmak gerekiyor; tartışmayı detaylandırmamak adına bu kanıtı geçiyorum.
Tekrar eden ve geçici durumları da tanımladıktan sonra 'Basit Rastgele Yürüyüş' modeline geri dönelim. Model farklı boyutlar için kesikli ya da sürekli olarak tanımlanabiliyor. Bir boyutta bir doğru üzerinde sağa ve sola doğru hareket edilirken, iki boyutta kafes (lattice) şeklinde bi yapı üzerine noktanın en yakınındaki dört komşusuna geçişler yaparak ilerleniyor. Üç boyut için komşu sayısı altıya çıkıyor ve bu böyle artarak devam ediyor. Bizim ilgilendiğimiz sürekli rastgele hareketler olacak. Problemimiz şu: Belirli bir noktadan başlayan bir rastgele yürüyüşçümüz tekrar bulunduğu noktaya geri döner mi? Bunu bize ünlü Polya Teoremi söylüyor.
Polya Teoremi: Köşeleri tam sayılardan oluşan d boyutlu $\mathbb{Z}^d$ kafesini (lattice) alalım. $\mathbb{Z}^d$ üzerinde simetrik rastgele hareket ($p = q = 1/2$):
1) $d \le 2$ için tekrar edendir.
2) $d \ge 3$ için geçicidir.
Polya teoremi bize simetrik rasgele hareketin başladığı noktaya yalnızca 1 ve 2 boyutta geri gelebileceğini, 3 ve daha fazla boyut için bunun kesin olmadığını, yürüyüşün başını alıp gidebileceğini söylüyor!
Kanıt:
1-boyutta, $\mathbb{Z}^1$'de, pozitif yönde bir adım atma olasılığı $p$, negatif yönde bir adım atma olasılığı $q$ olan, $p \not= q$ yürüyüşe bakalım. Orijinden $(j = 0)$ başlayan bir yürüyüşün tekrar geri gelmesi için sağ tarafa ve sol tarafa eşit sayıda adım atması gerekir, bu da toplam adım sayısının çift olmasını gerektirir. $2n$ adımda $0$ noktasından $0$'a geri gelme olasılığını şöyle yazabiliriz:
$$\mathbb{P}_{0,0}(2n) = \binom{2n}{n} p^n q^n \tag{5}$$
$2n \choose n$ $2n$ tane adımdan yarısını sağa, yarısını da sola olacak şekilde kaç farklı şekilde atabileceğimizi gösteren kombinatorik katsayı. Büyün $n$ sayıları için bu durumu incelediğimiz için $\binom{2n}{n}=\frac{(2n)!}{(n!)^2}$ ifadesi için meşhur Stirling yaklaşımını (Stirling's Approximation) kullanacağız:
$$n! \approx \sqrt{2 \pi n} \bigg( \frac{n}{e}\bigg)^n \hspace{1.5cm} \text{(Stirling yak.)} \tag{6}$$
$$ \binom{2n}{n}= \frac{(2n)!}{(n!)^2} \approx \frac{\sqrt{4 \pi n} \big( \frac{2n}{e}\big)^{2n}}{2 \pi n \big( \frac{n}{e}\big)^{2n}} = \frac{1}{\sqrt{\pi n} 4^n} $$ $$ \Rightarrow \mathbb{P}_{0,0}(2n) \approx \frac{1}{\pi n} (4 p q) ^n \tag{7}$$
Simetrik yürüyüş, yani $p = q = 1/2$ için:
$$\mathbb{P}_{0,0}(2n) \approx \frac{1}{\pi n} \tag{8}$$
Bu olasılıkların tüm $n$'ler için toplamını alıp $0$ durumunun tekrar edip etmeme şartına bakarsak $(4)$:
$$\sum_{n = 1}^{\infty} \mathbb{P}_{0,0}(2n) = \sum_{n = 1}^{\infty} \frac{1}{\pi n} = \infty \tag{9}$$
Sonucumuzu denklem $(4)$ ile karşılaştırdığımızda 1 boyutta simetrik rastgele yürüyüşün 'tekrar eden' bir yapıda olduğunu kanıtlamış olduk. $p \not= q$ için ise rastgele yürüşün 'geçici' yapıda olduğunu denklem $(7)$'de $p$ ve $q$'yu yerine koyup tüm $n$'ler üzerinden topladığınızda olasılığın sonlu çıkacağını göstererek kanıtlayabilirsiniz.
2-boyuta geldiğimizde ise, rastgele yürüyüşü sağ/sol yönünün yanında yukarı/aşağı olarak da yapıyor olacağız. Herhangi bir anda belirli bir konumda bulunan bir yürüyüş 1/4 olasılıkla sağa/sola ya da yukarı/aşağı hareket edebiliyor olacak (simetrik durum). Orijinden $(0)$ başlayan bir yürüyüşün aynı sebeplerden ötürü ancak çift sayıda adımda aynı noktaya geri gelebileceği bariz. İki boyutta da aynı noktaya geleceğinden dolayı, sağ/sol yönünde de, yukarı/aşağı yönünde de ayrı ayrı eşit sayıda adım atması gerekiyor. Toplamda $2n$ tane adımda $0$ noktasından başlayıp $0$'a geri gelen tüm adım dizilerinin her birinin olasılığı $\bigg( \frac{1}{4}\bigg)^{2n}$'dir. Peki bu adımlardan toplam kaç tane vardır?
$2n$ adımdan sağa $(n-k)$ tane, sola $(n-k)$ tane; yukarı $k$ tane ve aşağı $k$ tane olmak üzere kaç farklı şekilde adım atılabilir?
$$\binom{2n}{n-k, n-k, k, k} = \frac{(2n)!}{(n-k)! (n-k)! k! k!}$$
O halde oriinden başlayıp $2n$ adımda tekrar orijine geri gelme ihtimalini yazarsak:
\begin{align}
\mathbb{P}_{0,0} (2n) &= \sum_{k=0}^n \binom {2n}{n-k, n-k, k, k} \big( \frac{1}{4} \big)^{2n} \\ \\
&= \sum_{k=0}^n \frac{(2n)!}{(n-k)!^2(k!)^2 \big( \frac{1}{4} \big)^{2n} }\\ \\
&= \frac{(2n)!}{(n!)^2} \sum_{k=0}^n \frac{(n)!}{(n-k)!^2(k!)^2 \big( \frac{1}{4} \big)^{2n} }\\ \\
&= \binom{2n}{n} \sum_{k=0}^n \binom{n}{k}^2 \big(\frac{1}{4}\big)^{2n} = \binom{2n}{n}^2 \big(\frac{1}{4}\big)^{2n} \tag{10}
\end{align}
$(10)$'daki sonuç ifadesi 1-boyutta yürüyüş için bulduğumuz (5) olasılık değerinin $p = q = 1/2$ için karesi olduğu görülebilir.
$$\mathbb{P}_{0,0}(2n) = \bigg[ \bigg( \frac{1}{2} \bigg)^{2n} \binom{2n}{n} \bigg]^2 \approx \frac{1}{\pi n} \tag{11}$$
Bu olasılığı da tüm $n$ değerleri üzerinden toplarsak:
$$\sum_{n = 1}^{\infty} P_{0,0}(2n) \approx \frac{1}{\pi} \sum_{n=1}^{\infty} \frac{1}{n} = \infty \tag{12}$$
Olasılıkların toplamı 1-boyutta yürüyüş için olduğu gibi yine sonsuz çıktı. Tekrar etme koşulu $(4)$'e göre 2-boyutta yürümenin de tekrar eden bir yapıda olduğunu göstermiş olduk.
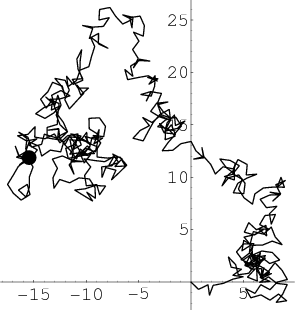 2-boyutta simetrik, eşit olasılıklar için kanıtladığımız tekrarlı olma özelliği olasılıkların simetrik olmadığı durumlar için geçerli değil. Bildiğim kadarıyla sadece sağ/sol ve yukarı/aşağı olasılıkların kendi içinde $1/2$'ye toplandıkları durum için de tekrarlı oluyor fakat diğer durumlar için muhtemelen(emin değilim) geçici özellikte.
2-boyutta simetrik, eşit olasılıklar için kanıtladığımız tekrarlı olma özelliği olasılıkların simetrik olmadığı durumlar için geçerli değil. Bildiğim kadarıyla sadece sağ/sol ve yukarı/aşağı olasılıkların kendi içinde $1/2$'ye toplandıkları durum için de tekrarlı oluyor fakat diğer durumlar için muhtemelen(emin değilim) geçici özellikte.Polya teoreminin en vurucu kısmı $d \ge 3$ için söyledikleri. Fakat buna bir sonraki yazıda değineceğiz.
(Solda: Orijinden başlayıp uzun bir süre ilerleyen 2 boyutlu bir rastgele yürüyüş simülasyonu görülüyor. Hareketin boyut arttıkça ne kadar karmaşıklaştığı açıkça görünüyor. Görüldüğü kadarıyla henüz orijine uğramamış. Kaynak: Wolfram)
2-boyutta rastgele hareketi biraz programlama (javascript) kullanarak kolayca kurcalamak isteyenlere şu sayfayı öneririm: p5.js Brownian Motion
