Stochastic Processes - IV Polya Teoremi

Notların dördüncü bölümünde Markov Zincir'lerinin birkaç özelliğinden daha bahsedip ilk notlarda konuyu açtığımız 'Basit Rastgele Yürüyüş' modeline geri dönüp Polya Teoremini gösterip epey ilginç sonuçlar elde edeceğiz. Öncelikle Markov Zincir'lerine dair birkaç tanım daha yapalım.

$\mathbb{X}$ yine $\mathcal{S}$ durum uzayına ve $P$ geçiş matrisine sahip bir Markov Zinrici olsun. Markov zinciri zamanla bir durumdan diğerine $P$'de verilen olasılıklarla geçiyor. Herhangi bir $j$ durumundan ilk kez geçtiği zamana 'ilk geçiş zamanı' olarak adlandıracağız ve bu zaman aşağıdaki gibi tanımlıyoruz:
$$T_j = min \{n \in\mathbb{N}: \hspace{0.5cm} X_n = j\} \tag{1}$$Markov Zinciri bu noktadan birden fazla kez (hatta sonsuz kere) geçiyor olabilir, biz bunların minimumunu alıp buna ilk geçiş zamanı $T_j$ diyoruz.

Soru: Eğer zincir $i$ durumundan başladığında, ileriki bir zamanda $i$'ye tekrar gelmek zorunda mı? Geliyorsa ne kadar sık geliyor?

Tanım: Bir $i$ durumu için
$$ \mathbb{P}(T_i < \infty) =  \mathbb{P}(T_i < \infty | X_0 = i) = 1 \tag{3}$$ ise $i$ durumuna 'tekrar eden' (recurrent) durum denir.

Tanım: Eğer bir durum 'tekrar eden' bir durum değilse ona 'geçici' (transient) durum denir.

Teorem: Bir $i$ durumu ancak ve ancak aşağıdaki şart sağlanıyorsa 'tekrar eden' bir durumdur:
$$\sum_{n = 0}^{\infty}  \mathbb{P}_{i, j}(n) = \infty \tag{4}$$Yukarıdaki ifadede $\mathbb{P}_{i, j}(n)$, terimi $i$ durumundan $j$ durumuna $n$ adımda geçme olasılığını gösteriyor. Eğer bir durum 'tekrar eden' bir durumsa, yani zincirin o duruma tekrar gelme ihtimali 1 ise, sonsuz adımda buraya sonsuz kere geleceğinden, tekrar tekrar geldiği adımlar için olasılıkları topladığımızda sonsuz elde edeceğiz. Bunu kanıtlamak için 'üreteç fonksiyonları' (generating functions) kullanmak gerekiyor; tartışmayı detaylandırmamak adına bu kanıtı geçiyorum.

Tekrar eden ve geçici durumları da tanımladıktan sonra 'Basit Rastgele Yürüyüş' modeline geri dönelim. Model farklı boyutlar için kesikli ya da sürekli olarak tanımlanabiliyor. Bir boyutta bir doğru üzerinde sağa ve sola doğru hareket edilirken, iki boyutta kafes (lattice) şeklinde bi yapı üzerine noktanın en yakınındaki dört komşusuna geçişler yaparak ilerleniyor. Üç boyut için komşu sayısı altıya çıkıyor ve bu böyle artarak devam ediyor. Bizim ilgilendiğimiz sürekli rastgele hareketler olacak. Problemimiz şu: Belirli bir noktadan başlayan bir rastgele yürüyüşçümüz tekrar bulunduğu noktaya geri döner mi? Bunu bize ünlü Polya Teoremi söylüyor.

Polya Teoremi: Köşeleri tam sayılardan oluşan d boyutlu $\mathbb{Z}^d$ kafesini (lattice) alalım. $\mathbb{Z}^d$ üzerinde simetrik rastgele hareket ($p = q = 1/2$):

1) $d \le 2$ için tekrar edendir.
2) $d \ge 3$ için geçicidir.

Polya teoremi bize simetrik rasgele hareketin başladığı noktaya yalnızca 1 ve 2 boyutta geri gelebileceğini, 3 ve daha fazla boyut için bunun kesin olmadığını, yürüyüşün başını alıp gidebileceğini söylüyor!

Kanıt: 

1-boyutta, $\mathbb{Z}^1$'de, pozitif yönde bir adım atma olasılığı $p$, negatif yönde bir adım atma olasılığı $q$ olan, $p \not= q$ yürüyüşe bakalım. Orijinden $(j = 0)$ başlayan bir yürüyüşün tekrar geri gelmesi için sağ tarafa ve sol tarafa eşit sayıda adım atması gerekir, bu da toplam adım sayısının çift olmasını gerektirir. $2n$ adımda $0$ noktasından $0$'a geri  gelme olasılığını şöyle yazabiliriz:
$$\mathbb{P}_{0,0}(2n) = \binom{2n}{n} p^n q^n \tag{5}$$
$2n \choose n$ $2n$ tane adımdan yarısını sağa, yarısını da sola olacak şekilde kaç farklı şekilde atabileceğimizi gösteren kombinatorik katsayı. Büyün $n$ sayıları için bu durumu incelediğimiz için $\binom{2n}{n}=\frac{(2n)!}{(n!)^2}$ ifadesi için meşhur Stirling yaklaşımını (Stirling's Approximation) kullanacağız:
$$n! \approx \sqrt{2 \pi n} \bigg( \frac{n}{e}\bigg)^n \hspace{1.5cm} \text{(Stirling yak.)} \tag{6}$$
$$ \binom{2n}{n}= \frac{(2n)!}{(n!)^2}  \approx \frac{\sqrt{4 \pi n} \big( \frac{2n}{e}\big)^{2n}}{2 \pi n \big( \frac{n}{e}\big)^{2n}}  = \frac{1}{\sqrt{\pi n} 4^n} $$ $$ \Rightarrow \mathbb{P}_{0,0}(2n) \approx  \frac{1}{\pi n} (4 p q) ^n \tag{7}$$
Simetrik yürüyüş, yani $p = q = 1/2$ için:
$$\mathbb{P}_{0,0}(2n) \approx \frac{1}{\pi n} \tag{8}$$
Bu olasılıkların tüm $n$'ler için toplamını alıp $0$ durumunun tekrar edip etmeme şartına bakarsak $(4)$:
$$\sum_{n = 1}^{\infty} \mathbb{P}_{0,0}(2n) =  \sum_{n = 1}^{\infty} \frac{1}{\pi n} = \infty \tag{9}$$
Sonucumuzu denklem $(4)$ ile karşılaştırdığımızda 1 boyutta simetrik rastgele yürüyüşün 'tekrar eden' bir yapıda olduğunu kanıtlamış olduk. $p \not= q$ için ise rastgele yürüşün 'geçici' yapıda olduğunu denklem $(7)$'de $p$ ve $q$'yu yerine koyup tüm $n$'ler üzerinden topladığınızda olasılığın sonlu çıkacağını göstererek kanıtlayabilirsiniz.

2-boyuta geldiğimizde ise, rastgele yürüyüşü sağ/sol yönünün yanında yukarı/aşağı olarak da yapıyor olacağız. Herhangi bir anda belirli bir konumda bulunan bir yürüyüş 1/4 olasılıkla sağa/sola ya da yukarı/aşağı hareket edebiliyor olacak (simetrik durum). Orijinden $(0)$ başlayan bir yürüyüşün aynı sebeplerden ötürü ancak çift sayıda adımda aynı noktaya geri gelebileceği bariz. İki boyutta da aynı noktaya geleceğinden dolayı, sağ/sol yönünde de, yukarı/aşağı yönünde de ayrı ayrı eşit sayıda adım atması gerekiyor. Toplamda $2n$ tane adımda $0$ noktasından başlayıp $0$'a geri gelen tüm adım dizilerinin her birinin olasılığı $\bigg( \frac{1}{4}\bigg)^{2n}$'dir. Peki bu adımlardan toplam kaç tane vardır?

$2n$ adımdan sağa $(n-k)$ tane, sola $(n-k)$ tane; yukarı $k$ tane ve aşağı $k$ tane olmak üzere kaç farklı şekilde adım atılabilir?
$$\binom{2n}{n-k, n-k, k, k} = \frac{(2n)!}{(n-k)! (n-k)! k! k!}$$
O halde oriinden başlayıp $2n$ adımda tekrar orijine geri gelme ihtimalini yazarsak:
\begin{align}
\mathbb{P}_{0,0} (2n) &= \sum_{k=0}^n \binom {2n}{n-k, n-k, k, k} \big( \frac{1}{4} \big)^{2n} \\ \\
&= \sum_{k=0}^n \frac{(2n)!}{(n-k)!^2(k!)^2 \big( \frac{1}{4} \big)^{2n} }\\ \\
&= \frac{(2n)!}{(n!)^2} \sum_{k=0}^n \frac{(n)!}{(n-k)!^2(k!)^2 \big( \frac{1}{4} \big)^{2n} }\\ \\
&= \binom{2n}{n} \sum_{k=0}^n \binom{n}{k}^2 \big(\frac{1}{4}\big)^{2n} = \binom{2n}{n}^2 \big(\frac{1}{4}\big)^{2n} \tag{10}
\end{align}
$(10)$'daki sonuç ifadesi 1-boyutta yürüyüş için bulduğumuz (5) olasılık değerinin  $p = q = 1/2$ için karesi olduğu görülebilir.
$$\mathbb{P}_{0,0}(2n) = \bigg[ \bigg( \frac{1}{2} \bigg)^{2n} \binom{2n}{n} \bigg]^2 \approx \frac{1}{\pi n} \tag{11}$$
Bu olasılığı da tüm $n$ değerleri üzerinden toplarsak:
$$\sum_{n = 1}^{\infty} P_{0,0}(2n) \approx  \frac{1}{\pi} \sum_{n=1}^{\infty} \frac{1}{n} = \infty \tag{12}$$
Olasılıkların toplamı 1-boyutta yürüyüş için olduğu gibi yine sonsuz çıktı. Tekrar etme koşulu $(4)$'e göre 2-boyutta yürümenin de tekrar eden bir yapıda olduğunu göstermiş olduk.

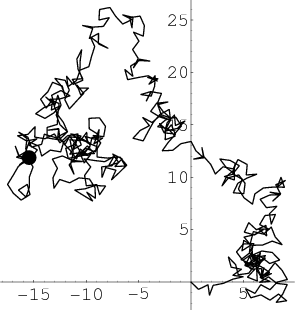2-boyutta simetrik, eşit olasılıklar için kanıtladığımız tekrarlı olma özelliği olasılıkların simetrik olmadığı durumlar için geçerli değil. Bildiğim kadarıyla sadece sağ/sol ve yukarı/aşağı olasılıkların kendi içinde $1/2$'ye toplandıkları durum için de tekrarlı oluyor fakat diğer durumlar için muhtemelen(emin değilim) geçici özellikte.

Polya teoreminin en vurucu kısmı $d \ge 3$ için söyledikleri. Fakat buna bir sonraki yazıda değineceğiz.

(Solda: Orijinden başlayıp uzun bir süre ilerleyen 2 boyutlu bir rastgele yürüyüş simülasyonu görülüyor. Hareketin boyut arttıkça ne kadar karmaşıklaştığı açıkça görünüyor. Görüldüğü kadarıyla henüz orijine uğramamış. Kaynak: Wolfram)


2-boyutta rastgele hareketi biraz programlama (javascript) kullanarak kolayca kurcalamak isteyenlere şu sayfayı öneririm: p5.js Brownian Motion

Stochastic Processes - III ( Chapman-Kolmogorov denklemi)

Notların üçüncü bölümünde Stochastic Process'ler konusunda önemli bir denklem olan Chapman-Kolmogorov denklemini ele alacağız. Öncesinde Markov süreçlere dair temel birkaç tanım yaptıktan sonra denklemi ifade edip, çözümüne dair birkaç laf ederek sonunda 'Master Equation' olarak adlandırılan önemli bir denklemi elde edeceğiz.

(NOT: Bu yazıda farklı bir kaynaktan yararlandığım için serinin diğer yazılarından biraz farklı bir notasyon kullandım. Kaynağım V. Balakrishan'ın 'Physical Applications of Stochastic Processes' ders videoları (Lecture 6).)

Elimizde zamanla farklı durumlar arasında 'dolaşan' bir süreç var ve bu süreci gözleyerek zaman serisi şeklinde veriler elde ediyoruz. $\mathbb{X}$ olarak adlandıracağımız bu sürecin durum uzayı ${j_1, j_2, ...}$ (ve kimi zaman da $k$ ve $l$ olarak) ve zaman örnekleri de ${t_1, t_2, ...}$ şeklinde etiketlensin. $\mathbb{X}$ sürecini tanımlayabilmemiz için $j_1$'den başlayıp $n$ adım sonunda $j_n$ durumuna gelen zincir için şu olasılığı yazabilmemiz gerekir:
$$P_n(j_n, t_n; j_{n-1}, t_{-1};...;j_1, t_{-1}) \tag{1}$$ $P_n$ ifadesindeki $n$ kaç adımlık bir olasılık yazdığımızı gösteriyor.

Bu ifadeyi koşullu olasılıklar şeklinde yazarsak şunu elde ederiz:
$$P_n(j_n, t_n; j_{n-1}, t_{-1};...;j_1, t_{-1}) = P_n(j_n, t_n| j_{n-1}, t_{n-1}; ...; j_1, t_1) P_{n-1}(j_{n-1}, t_{n-1}; ... ; j_1, t_1) \tag{2}$$
Üstteki iki olasılık ifadesinden ilki ($P_n$) terimi, fiziksel bir varsayımda bulunursak epey sadeleşiyor; bu da gözlemlediğimiz çoğu sürecin eğer yeteri kadar değişken kullandığımız takdirde bir sonraki adımı, sadece bir önceki adımına bağlı, geçmişteki tüm durumlarından bağımsız olması. Buna Markov özelliği diyoruz. Bu durumda ilk terim şu şekilde sadeleşiyor:
$$P_n(j_n, t_n| j_{n-1}, t_{n-1}; ...; j_1, t_1) = P_2(j_n, t_n|j_{n-1}, t_{n-1}) \tag{3}$$
Markov varsayımını kullandığımızda $(1)$'i aşağıdaki gibi iki adımlık olasılıkların çarpımı şeklinde yazabiliyoruz:
$$P_n(j_n, t_n; j_{n-1}, t_{-1};...;j_1, t_{-1}) = \big(\prod_{r=1}^{n-1}P_2(j_n, t_n|j_{n-1}, t{n-1})\big)P_1(j_1, t_1) \tag{4}$$
Zincirin yapısı gereği, zamanla durumların istatistiklerinin değişmediği yani zincirin evriminin zamana özel olarak bağlı olmadığı süreçleri durağan (stationary) süreçler olarak tanımlıyoruz. Durağanlık, iki durum arası geçiş olasılıklarının her bir durumun ilgili zamanı yerine, iki durumun zaman farklarına bağlı olmasına neden oluyor. Yani hangi zamanlarda değil de aralarında ne kadar zaman farkı ile geçtikleri önem kazanıyor.
$$P_2(k,t|j, t') = f(t-t')$$
Sadece arada geçen zaman önemli olduğuna göre zamanın başlangıç noktasını kaydırarak (bir önceki yazıdaki Markov zincirlerinin zamanda homojen olma özelliğini kullanarak) bu olasılığı şöyle ifade edebiliriz:
$$P_2(k,t|j, t')  = P_2(k, t-t'|j, 0) \equiv P_2(k, t- t'|j) \tag{5}$$
Son adımda başlangıç zamanı $0$'ı notasyondan çıkardık ve bundan sonra verilmediği her durum için $0$'dan başladığını düşünüyoruz. Bu tanımlamalar altında $(1)$ denklemini aşağıdaki gibi ifade ediyoruz: $$P_n(j_n, t_n; j_{n-1}, t_{-1};...;j_1, t_{-1}) = \big(\prod_{r=1}^{n-1}P_2(j_{r+1}, t_{r+1} - t_r|j_r)\big) P_1(j) \tag{6}$$
Son olarak zamanda ilerledikçe ($t \to \infty$) $P(k, t| j)$'nin başlangıç durumu $j$'den bağımsızlaşacağını ve durağan duruma eriştiğinde erişilen durumun durağan olasılığına eşit olacağını varsayıyoruz; kısacası zincir yeteri kadar beklendiğinde geçiş hafızasını tamamen unutuyor. Bu durum Markov zincirlerinde 'mixing' (karışma) şeklinde ifade ediliyor. Kısacası elimizdeki olasılıklar şuna indirgeniyor: $$ P(k, t |j) \longrightarrow P(k)$$
Bu şartlar altında zincirin ilk başta $j$ durumundayken, $t$ kadar süre sonra $k$ konumunda olma olasılığını şu şekilde yazabiliriz:
$$\boxed{ P(k, t|j) = \sum_{l = 1}^N P(k, t - t'| l) P(l, t'|j)}  \tag{7}$$
Bu denklem bize şunu söylüyor: Eğer $j$'den $k$'ya gitme olasılığını hesaplamak istiyorsak, aradaki her bir $l$ durumundan geçme olasılıklarını bulup çarparak sonuca erişiyoruz. Bu denklem 'Chapman-Kolmogorov Denklemi' olarak biliniyor. Denklem iki olasılık çarpımından oluşuyor; olasılıklara göre doğrusal olmayan (nonlinear) bir denklem olduğundan hesaplaması oldukça güç. Bunu doğrusal bir şekilde yazabilsek hayat çok daha kolaylaşacak. Bunun için de durumların birim zamanda birbirine ortalama geçiş sayısını belirten bir parametre olarak 'geçiş oranı' (transition rate) $w(k,j)$ tanımlıyoruz.
$$P(k, \delta t|j) = w(k|j)\delta t\hspace{1.5cm} k \not= j \tag{8}$$
Kolmogorov-Chaapman denklemindeki geçiş olasılıkları yerine $(8)$'deki ifadeyi yerleştirip $t - t' = \delta t$ olarak aldığımızda aşağıdaki diferansiyel denklemi elde ederiz.
$$ \boxed{\frac{d}{dt} P(k, t |j) =  \sum_{l = 1}^N \big[ w(k,l)P(l,t|j) - w(l,k)P(k,t|j)\big]} \tag{9}$$
Bu denklem 'Master Equation' olarak adlandırılıyor. Görüldüğü gibi $(9)$ birinci dereceden bir diferansiyel denklem. $(7)$'deki doğrusal olmayan terim yerine $P$'nin doğrusal terimleri var artık denklemde. Sağdaki toplam, tüm $l$ ara durumları üzerinden yapılıyor. Denklemin sağ tarafında toplam içindeki terim $j$'den önce ara durum olan $l$'ye, ardından nihai durum $k$'ya geçişi yani olasılıktaki artışı(gain term); ikincisi ise önce $j$'den nihai durum $k$'ya, ardından ara durumlardan biri olan $l$'ye geçişi yani olasılıktaki azalmayı (loss term) veren terimler.

Böylece elimizdeki Markov Zinciri'nin başlangıçtaki bir durumdan $t$ kadar süre sonra başka bir duruma geçme olasılığının zamanla değişimini veren bir denklem elde etmiş olduk.

Stochastic Processes - II

Notlarımızın ikinci kısmına basit bir toplam 2 duruma sahip basit bir Markov Zinciri'ni inceleyerek başlayalım. Elimizde, 1 ve 2 ile etiketlenmiş iki duruma sahip bir Markov Zinciri olsun; durumlar arasındaki geçişler de aşağıdaki diyagramda gösterildiği gibi verilmiş olsun. Okların üzerinde yazan sayılar geçiş olasılıklarını versin.

Zincirin geçiş matrisi $P$'yi şu şekilde yazabiliriz: $$ \begin{pmatrix} 1- \alpha & \alpha \\ \beta & 1 - \beta \end{pmatrix}$$
$\alpha, \beta \in (0,1)$. Geçiş  matrisini başlangıç olasılık dağılımı ($\lambda_0$) ile çarparak bir sonraki adımlardaki dağılımları elde ediyoruz. $$ P \lambda_0 = \lambda_1 \\ P \lambda_1 = \lambda_2 = P^2 \lambda_0 \\ ... \\ P^n \lambda_0 = \lambda_n $$
$P^n$ matrisinin büyük $n$ değerleri için nasıl davranacağını anlamak için, $P$'yi orthogonalize edip özdeğer (eigenvalue) ve özvektörlerini (eigenvecor) bulalım.
$$\text{det} (P - \nu \mathbb{I}) = \begin{vmatrix} 1- \alpha - \nu & \alpha \\~\\ \beta & 1 - \beta - \nu \end{vmatrix} = 0 \\~\\ (1- \alpha - \nu) (1 - \beta - \nu) -\alpha \beta = 0 \\~\\ \nu_{1,2} = \frac{2 - \alpha - \beta \pm (\alpha + \beta)}{2}$$
Bu denklemlerden iki özdeğeri $\nu_1 = 1$, karşılık gelen özvektörü $\begin{bmatrix} 1 \\ 1 \end{bmatrix} $ ve $\nu_2 = 1- \alpha - \beta$, karşılık gelen özvektörü de $\begin{bmatrix} - \alpha \\ \beta \end{bmatrix}$ olarak elde ederiz.

$\nu_1 = 1$ değeri sonradan göreceğiz ki Markov Zinciri'nin uzun vadede durağan dağılımını veren özdeğer olacak. $$\lambda^* P = 1 \lambda^* \hspace {1cm} (\lambda^* \hspace{0.2cm} \text{durağan dağılım})$$
$P$'nin $n$. kuvvetini alabilmek için orthogonalleştirmeye çalışıyorduk. Bunun için $M$, $M^{-1}$ ve $D$ matrislerini oluşturmamız gerekiyor: $$ P = M D M^{-1}$$
$M$ matrisi kolonları $P$'nin özvektörleri, $D$ matrisi de $P$'nin özdeğerlerini köşegenlerinde bulunduran matris; $M^{-1}$ de $M$ matrisinin tersi.
$$M = \begin{pmatrix} 1 & \alpha \\ 1 & \beta \end{pmatrix} \hspace{0.5cm} D = \begin{pmatrix} 1 &0 \\ 0 & 1- \alpha - \beta \end{pmatrix}\hspace{0.5cm} M^{-1} = \frac{1}{\beta + \alpha} \begin{pmatrix} \beta & \alpha \\ -1 & -1 \end{pmatrix}$$
$$P^n = (M D M^{-1})^n = M D^n M^{-1} = \frac{1}{\alpha + \beta} \begin{pmatrix} 1 & \alpha \\ 1 & \beta \end{pmatrix} \begin{pmatrix} 1^n &0 \\ 0 & (1- \alpha - \beta)^n \end{pmatrix} \begin{pmatrix} \beta & \alpha \\ -1 & -1 \end{pmatrix} \\~\\ \\~\\  P^n= \frac{1}{\alpha + \beta}\begin{pmatrix} \beta + \alpha(1-\alpha-\beta)^n & \alpha - \alpha (1-\alpha-\beta)^n \\ \beta - \beta(1-\alpha-\beta)^n & \alpha +  \beta(1-\alpha-\beta)^n \end{pmatrix} $$
İlgilendiğimiz soru, büyük $n$ değerleri için ($n \to \infty$) $P^n$ matrisinin nasıl davranacağı. $n$'i sonsuza götürdüğümüzde matriste parantez içindeki üslü terimler sıfıra gidecekler çünkü $(1 - \alpha + \beta) \in (-1, 1).$ $$\lim_{n\to\infty} P^n = \begin{pmatrix} \frac{\beta}{\alpha+\beta} & \frac{\alpha}{\alpha+\beta}  \\ \frac{\beta}{\alpha+\beta}  & \frac{\alpha}{\alpha+\beta}  \end{pmatrix} = P^{\infty}$$
Bu limite bakarak belirli bir zaman geçtikten sonra, durumlar arasındaki geçişlerin dengeye oturacağını ve geçiş olasılıklarının sabitleneceğini görüyoruz. Bu durum $n \to \infty$ için Markov zincirinin bir durağan dağılıma erişiyor olmasıyla da ilişkili. İleriki bölümlerde buna da detaylıca değineceğiz.